предмет и задачи внешней баллистики

RAAAR.RU

Сегодня 16.04.2018 : Monday
Время на сервере: 21:59

Меню сайта:

При копировании материалов
ссылка на этот ресурс обязательна.

1. предмет и задачи внешней баллистики

Внешней баллистикой называется наука о движении снарядов (пуль) и ракет после вылета их-из канала ствола или схода с направляющих. До сравнительно недавнего времени баллистика изучала почти исключительно движение снаряда постоянной массы. Качественное изучение движения ракет являлось предметом специальных разделов механики (механика тел переменной массы). И только в связи с бурным развитием ракетной техники в годы, предшествовавшие второй мировой войне, и особенно после нее, наука о движении ракет стала неотъемлемой частью баллистики и даже вылилась в самостоятельную науку. Поскольку, однако, ствольное оружие в основном стреляет снарядами постоянной массы, в настоящей книге излагаются вопросы, связанные с их движением. Простейшие случаи движения ракет описываются в виде дополнения к соответствующим разделам.
Конечной целью предмета внешней баллистики является составление таблиц стрельбы, позволяющих расчету правильно наводить орудие на цель с учетом конкретных (главным образом атмосферных) условий стрельбы, а также определение исходных данных для проектирования орудий и снарядов. Решению этих задач предшествует изучение закономерностей движения тяжелого тела в воздухе.
На выброшенное под углом к горизонту и с определенной скоростью тело действует сила тяжести и комплекс аэродинамических сил и моментов. Изучение закономерностей изменения сил, действующих на снаряд в полете, является одной из задач внешней баллистики.
Движение продолговатого снаряда, обладающего шестью степенями свободы, описывается системой дифференциальных уравнений двенадцатого порядка с неразделяющимися переменными. Даже при известных силовых факторах решение такой системы крайне трудоемко и неудобно для практического использования.
При этом иногда возникают непреодолимые трудности экспериментального и теоретического определения отдельных составляющих аэродинамических сил, связанные с их нестационарностью. Даже важнейшие составляющие аэродинамических сил приходится принимать по усредненным значениям. Поэтому целесообразно движение центра масс снаряда и движение его около центра масс изучать раздельно, вводя в дальнейшем экспериментальные коэффициенты согласования с опытом. Часть коэффициентов (например, коэффициент или функция лобового сопротивления) оказывается при этом достаточно универсальной, относящейся к большому классу снарядов. Другая часть (например, коэффициент формы снаряда) отражает индивидуальные свойства снарядов определенного образца.
Существенную роль в пространственном положении траектории снаряда играют многочисленные случайные или неучитываемые в уравнениях движения факторы. К числу первых относятся, например, отклонения масс снарядов от номинального значения, вызванные технологическими погрешностями; массовая и химическая неоднородность зарядов; изменение метеорологических условий. Из неучитываемых факторов отметим влияние кривизны и вращательного движения земного шара, особенно заметное при движении дальнобойных снарядов.
Если факторы влияют на полет снаряда систематически, то положение траектории в пространстве может быть исправлено путем изменения начальных данных. Так, при подготовке стрельбы из крупнокалиберной артиллерии все снаряды разбиваются на группы по массе, одинаковой в определенных пределах, тщательно изучаются метеорологические условия с тем, чтобы скорректировать установку прицельных приспособлений. Раздел внешней баллистики, изучающий отклонения траекторий от расчетной под влиянием известных по величине (и направлению) факторов, называется теорией поправок.
Учет большого числа факторов, влияющих на отклонение траекторий, оказывается либо невозможным, либо нецелесообразным. Невозможно заранее предугадать, например, отклонение угла вылета снаряда, вызванное колебаниями ствола и орудия в целом. Экономически нецелесообразно разбивать на группы по массе пули стрелкового оружия. Распределение точек попадания выступает в этом случае как случайная величина.
Определение коэффициентов согласования с опытом, предшествующее составлению таблиц стрельбы (или проектированию прицельных приспособлений), в силу сказанного, требует многократного повторения эксперимента. Необходимо иметь свод правил, обеспечивающих получение надежных результатов при минимальном числе стрельб.
Таким образом, основное содержание баллистики ствольных систем составляют следующие задачи.1.   Изучение аэродинамических сил, действующих на снаряд в полете. При этом должна быть найдена форма снаряда, обеспечивающая без существенного ослабления могущества действия его у цели минимальное сопротивление воздуха и, следовательно, максимальную дальность полета.
2.   Изучение траектории движения центра масс снаряда в воздухе— основная задача внешней баллистики. Прямая задача заключается в определении параметров траектории по заданным начальным данным. Обратная задача — в определении одного из начальных параметров по установленным координатам точки падения снаряда (координатам цели). Могут быть и специальные задачи, когда, например, нужно обеспечить не только попадание в цель, но и достижение требуемой скорости встречи снаряда с целью.
3.   Изучение движения снаряда около центра масс с целью обеспечения устойчивости снаряда на траектории.
4.   Разработка теории поправок, позволяющей учесть влияние на траекторию некоторых известных по величине факторов, изменяющихся от выстрела к выстрелу или от стрельбы к стрельбе.
5.   Изучение рассеивания снарядов под воздействием случайных факторов и влияния этого рассеивания на результаты стрельбы; разработка методики составления таблиц стрельбы.
6.   Нахождение оптимального решения задач внешней баллистики на основе заданных тактико-технических требований при проектировании новых образцов оружия.
Для решения перечисленных задач постоянно применяются наиболее современные и эффективные методы экспериментальных и теоретических исследований. Важное прикладное значение теории полета снаряда побуждало многих математиков и физиков всех времен уделять значительное внимание развитию внешней баллистики.

2. краткие сведения из истории внешней баллистики

Простейшие метательные орудия — праща, лук со стрелами — были известны человеку с глубокой древности. Довольно высокая меткость этих орудий обеспечивалась навыками и искусством стрелка. По мере развития и усложнения метательной техники, появления тяжелых баллист и катапульт совершенствовались и эмпирические правила наведения орудий на цель.Первую попытку осмыслить законы движущегося в воздухе тела сделали философы античности в своем стремлении создать общую картину мироздания. Аристотель (384—322 гг. до н. э.) выдвинул сложную и противоречивую теорию движения тел, брошенных под углом к горизонту. Архимед (287—212 гг. до н. э.) — творец совершеннейших по тому времени военных метательных машин — первым дал конкретное представление о форме траектории снаряда. Он считал, что брошенное под углом к горизонту тело движется по спирали. Несмотря на созерцательный характер мировозрения авторов античности, их исследования в области механики и геометрии явились тем фундаментом, на котором много веков спустя развились наиболее плодотворные идеи механики и, в частности, баллистики.

В середине XIV в. философом Парижского университета Буриданом была предложена новая теория «импетуса», господствовавшая в механике два столетия. Эту теорию' развивали и пропагандировали такие выдающиеся ученые, как Леонардо да Винчи и Галилей. Импетус — прообраз современного понятия о количестве движения, хотя его смысл не отражал законов движения тел, тогда еще не открытых, а основывался на чисто геометрических соображениях.
Леонардо да Винчи на основании теории импетуса исследовал вопрос о форме траектории снаряда в воздухе, которую он представлял в виде начального прямолинейного и последующего криволинейного участков, хотя в записках ученого был обнаружен чертеж траектории в виде параболы. Леонардо да Винчи обратил внимание на необходимость учитывать влияние сопротивления воздуха на движение снаряда и высказал некоторые соображения о величине этого сопротивления.
В XVI в. огнестрельная артиллерия прочно вошла в состав вооружения армий. Артиллерийская практика настоятельно требовала разработки надежных и простых методов составления таблиц стрельбы, уточнения некоторых эмпирических правил.
Становление внешней баллистики как прикладной науки связано с именем итальянского ученого Тартилья, опубликовавшего в 1537 г. фундаментальный труд под названием «Новая наука». В основе его представлений о траектории лежала теория импетуса. Исследуя свойства траектории, Тартилья первым установил пропорцию, связывающую дальность полета снаряда с начальным углом вылета. Знание этой пропорции во много раз сокращало количество опытных стрельб, необходимых для составления таблиц стрельбы (сам Тартилья утверждал, что для составления таблиц требуется всего один выстрел — о рассеивании снарядов еще не было известно). Тартилья первым обнаружил, что наибольшая дальность в случае стрельбы тяжелыми снарядами получается при угле бросания 45°. Траектория Тартильи и разработанные им правила составления таблиц стрельбы вошли в руководства по артиллерии всех стран и просуществовали в них более ста лет вплоть до признания артиллеристами трудов Галилея. В русские артиллерийские руководства таблицы Тартильи вошли после изложения его теории в «уставе ротных, пушечных и других дел», написанном О. Михайловым в 1606—1620 гг.

Исследования в области механики Галилей начал с изучения падения тяжелых тел. Свои теоретические рассуждения он подкрепил опытами, бросая шары из различных материалов с башни и спуская их по наклонной плоскости. Эти опыты положили начало экспериментальной физике. В результате Галилей установил равноускоренное движение падающих тел, о котором его предшественники (в частности, Леонардо да Винчи) смутно догадывались. В изданном в 1638 г. трактате «Беседы» Галилей, разложив движение тела, брошенного параллельно горизонту, на равномерное горизонтальное и равноускоренное вертикальное, доказал, что траектория такого движения является параболой. Несколько позже (1644) Торичелли распространил это доказательство на более общий случай бросания тел под углом к горизонту.
Изучением сопротивления воздуха занимались многие ученые того времени, в том числе Декарт и Гюйгенс, однако окончательная формулировка задачи принадлежит Ньютону. Он исходил из того, что воздух представляет собой совокупность равномерно распределенных и не связанных между собой частиц. При ударе о поверхность эти частицы получают определенную кинетическую энергию, затормаживая тем самым движение тела. Применив уравнения количества движения и сохранения кинетической энергии, Ньютон установил (1687), что сопротивление воздуха пропорционально квадрату скорости движения тела, площади его поперечного сечения и плотности воздуха. Сейчас известно, что квадратичный закон сопротивления справедлив для дозвуковых скоростей. Коэффициент пропорциональности Ньютон определял из опыта. Ньютон впервые поставил вопрос об образующей тела вращения, обеспечивающей наименьшее сопротивление воздуха, и провел первое исследование в этой области. В разное время над решением этого вопроса работали такие выдающиеся ученые, как Иоганн Бернулли, Лопиталь, Эйлер и Лагранж. Он не перестает быть актуальным и в наши дни.

Разработка теории движения снаряда при квадратичном законе сопротивления велась учеными Германом, Бернулли и нашла свое теоретическое завершение в трудах Эйлера. Считая плотность воздуха неизменной по высоте, Эйлер проинтегрировал уравнение годографа скорости, после чего нахождение координат центра тяжести снаряда свелось к квадратурам. На основании метода Эйлера и более поздних его усовершенствований многими авторами были составлены таблицы стрельбы, среди которых наибольшую известность получили таблицы Отто (1883). Большое значение для развития баллистики имели полученные Эйлером дифференциальные уравнения движения твердого тела, которые легли в основу теории движения снаряда около центра масс.
Квадратичная зависимость закона сопротивления от скорости вызвала сомнение уже у физиков XVIII в. Талантливым английским экспериментатором Робинсоном был изобретен баллистический маятник и в 1740 г. были опубликованы первые опыты по определению силы сопротивления воздуха стрельбой. Эти опыты показали, что квадратичный закон сопротивления справедлив только для скоростей до 240 м/с (для сферических снарядов). По мере увеличения скорости снаряда закон сопротивления все более отклоняется от квадратичного. Опыты эти были известны Эйлеру,, и он попытался внести соответствующие коррективы в свой метод. Однако квадратичный закон долгое время оставался основным в баллистических исследованиях. Окончательный отказ от него- произошел только во второй половине XIX в. в связи с резким увеличением мощности огнестрельного оружия и переходом на нарезную артиллерию со стрельбой продолговатыми снарядами. Надо было изучать сопротивление воздуха в широком диапазоне скоростей, а для определения условий устойчивого полета снаряда необходимо было изучить его движение около центра масс.

Выдающуюся роль в развитии баллистики продолговатых снарядов сыграл русский артиллерист и ученый Н. В. Маиевский (1823—1892), первые научные работы которого были посвящены баллистике сферических снарядов. В 1858—1859 гг. под непосредственным руководством Маиевского проводились сравнительные стрельбы из гладкоствольных и нарезных орудий, выявившие полное преимущество последних. Эти испытания способствовали принятию нарезных орудий на вооружение русской армии. С тех пор вся дальнейшая научная деятельность Маиевского была связана с изучением проблем движения вращающегося артиллерийского снаряда. Первая его работа по этому вопросу «О влиянии вращательного движения на полет продолговатых снарядов в воздухе», опубликованная в 1865 г., получила широкое признание не только в России, но и за границей. В 1867 г. за эту работу Маиевскому была присуждена большая Михайловская премия (первую такую премию Маиевский получил в 1858 г. за труд <Ю давлении пороховых газов на стены орудия и о приложении результатов опытов, проведенных на этот предмет в Пруссии, к расчету толщины стен орудий»).
Опыты Маиевского (1868—1869) по изучению сопротивления воздуха движению снарядов различного типа позволили получить известные формулы. Сопротивление воздуха было представлено в виде степенной зависимости, показатель которой принимает различные значения в определенных диапазонах скоростей (зональный закон сопротивления). Эти формулы положили начало новой, эпохи в развитии внешней баллистики и вскоре стали известны далеко за пределами России.
Помимо научной деятельности, Маиевский принимал непосредственное участие в разработке новых образцов нарезных орудий, превосходивших аналогичные иностранные орудия. Некоторые из этих образцов были приняты на вооружение и за границей.
Велики заслуги Маиевского в деле подготовки русских артиллерийских офицеров и ученых. Написанный им в 1870 г. «Курс внешней баллистики» оставался длительное время лучшим в мировой литературе, а в некоторых разделах сохраняет актуальность и по сей день. Заслуги генерала от артиллерии заслуженного ординарного профессора Михайловской Артиллерийской Академии
Н. В. Маиевского были высоко оценены его современниками, он был награжден многими русскими орденами, избирался почетным членом Михайловской Артиллерийской академии и Московского университета. В 1878 г. Н. В. Маиевский был избран членом-кор- респондентом Петербургской академии наук.
Труды Маиевского были развиты его учеником и преемником по должности профессора кафедры баллистики Михайловской Артиллерийской академии Н. А. Забудским (1853—1917). Забудский первым в мире получил расчетную формулу для определения крутизны нарезов, обеспечивающей устойчивость снаряда в полете, продолжил опыты Маиевского по определению закона сопротивления воздуха, установив этот закон в диапазоне скоростей 700—1000 м/с. В 1895 г. Забудский издал курс «Внешняя баллистика», в котором' отразил итоги работ в области баллистики за несколько лет. Большое значение для дальнейшего развития баллистики имела другая его работа «Теория вероятностей и ее применение к стрельбе и пристрелке» (1898), в которой были заложены основы теории поправок.

Опыты по определению силы сопротивления воздуха проводились одновременно во многих странах. В Англии в 1866—1870 гг. велись эксперименты с продолговатыми снарядами калибра 7,62—299 мм в диапазоне скоростей 230—520 м/с. В 1884 г. Хой- хель в Голландии производил опыты со. снарядами калибра 80—400 мм. В 1879—1896 гг. фирмой Крупп были испытаны снаряды большого удлинения в диапазоне скоростей 150—910 м/с.
В 1896 г. итальянским ученым-артиллеристом Сиаччи были систематизированы все опубликованные к тому времени результаты опытов по определению закона сопротивления воздуха и предложена формула, выражающая этот закон. Функция лобового сопротивления (коэффициент при квадрате скорости) Сиаччи была принята во многих странах, в том числе и в России, и просуществовала без изменений вплоть до 20—30-х годов нашего столетия. Еще раньше, в 1880 г., Сиаччи разработал приближенный аналитический метод решения задачи внешней баллистики для прицельной стрельбы, не потерявший значения до настоящего времени.
Особенно бурное развитие получила внешняя баллистика после Великой Октябрьской Социалистической революции. В 1918 г. решением Советского правительства была создана постоянно действующая комиссия особых артиллерийских опытов (КОСАРТОП). Комиссия обобщала опыт первой мировой войны, определяла перспективы развития артиллерии, изучала физику процессов и уточняла зависимости внешней и внутренней баллистики. В ней плодотворно трудились крупнейшие ученые-артиллеристы В. М. Трофимов (председатель), Н. Ф. Дроздов, Г. П. Киснемский, академики А. Н. Крылов, Н. Е. Жуковский, С. А. Чаплыгин. Руководя работой комиссии, В. М. Трофимов (1865—1926) исследовал и опубликовал актуальные вопросы стрельбы и баллистики, разработал проект пушки для сверхдальней стрельбы (на дальность оолее 100 км). Из ранних работ В. М. Трофимова следует отметить груды «О теоретическом определении вероятных отклонений отчельных траекторий от средней» (1895 г., отмечен малой Михайловской премией) и «Действие шрапнели при стрельбе из трехдюймовой полевой пушки» (1903 г., удостоен премии генерала Рассказова и большой Михайловской премии).
В перечне трудов знаменитого русского теоретика кораблестроения акад. А. Н. Крылова видное место занимают работы по артиллерии. Среди них статья «Об организации управления артиллерийским огнем и опытах для .определения меткости судового огня», (1909), исследования по применению индикатора Уатта для записи давления пороховых газов в канале ствола, исследования по колебаниям стволов и др. Однако наиболее значительные работы в области баллистики относятся к периоду деятельности А. Н. Крылова в КОСАРТОПе. В 1920 г. им разработан метод численного решения уравнений внешней и внутренней баллистики, широко применявшийся для составления таблиц стрельбы вплоть до появления быстродействующих ЭВМ. В связи с необходимостью увеличения дальности стрельбы и проектированием сверхдальнобойной артиллерии возникла проблема обеспечения устойчивости снаряда вблизи вершины траектории, особенно при движении в разреженных слоях атмосферы.
При решении этой проблемы A. Н. Крылов применил оригинальный способ составления и интегрирования уравнений движения снаряда около центра масс, впоследствии развитый профессором Б. Н. Окуневым.

Академиками Н. Е. Жуковским и С. А. Чаплыгиным исследовался вопрос о наивыгоднейшей форме снаряда, возникший после первой мировой войны в связи с необходимостью увеличения дальности стрельбы существующих орудий. Он был успешно решен в КОСАРТОПе. Так, дальность стрельбы трехдюймовой полевой пушки благодаря улучшению аэродинамической формы снаряда была увеличена с 8 до 12 км.
Профессор Д. А. Вентцель в основном завершил разработку современной теории поправок. Он же описал движение снаряда около центра масс с учетом всех составляющих аэродинамических сил и моментов, а также создал теорию движения около центра масс оперенных снарядов. С 1927 г. в Советском Союзе при составлении таблиц стрельбы используют «нормальную атмосферу», предложенную Д. А. Вентцелем на основании статистической обработки метеорологических данных за много лет.
Большой вклад в развитие внешней баллистики внес акад.
B. С. Пугачев. Им были решены совместно шесть дифференциальных уравнений, которыми описывается движение снаряда как твердого тела. Были разработаны новые, более совершенные методы численного интегрирования, улучшена методика составления таблиц стрельбы наземной, зенитной артиллерии и стрелкового оружия.
В 20-х годах нашего столетия, в связи с переходом на снаряды новой формы, во многих странах проводились опыты по уточнению закона сопротивления воздуха. Наиболее известными являются опыты Гаврской комиссии (научно-исследовательский орган морской артиллерии), проведенные в 1921 —1923 гг. Обработав результаты этих опытов, Гарнье выразил закон сопротивления в виде двух функций для дозвуковых и сверхзвуковых скоростей. В месте перехода от одной функции к другой образуется угловая точка, что не согласуется с физическими представлениями о законе сопротивления и является недостатком закона Гарнье. В 1930 г. коллектив кафедры внешней баллистики Артиллерийской академии им. Дзержинского заново обработал результаты опытов Гаврской комиссии и предложил закон сопротивления в виде таблиц, получивший название «закона 1930 г.» В конце 30-х годов были начаты опыты по определению закона сопротивления для снарядов сложившейся к тому времени формы. Эти опыты были завершены уже в период Великой Отечественной войны и представлены в виде табличного закона, получившего название «закона 1943 г.». Был существенно уточнен закон сопротивления для скоростей в диапазоне 1000—2000 м/с. Уменьшение абсолютного значения функции лобового сопротивления (рис. 1) свидетельствует об улучшении аэродинамических форм снарядов.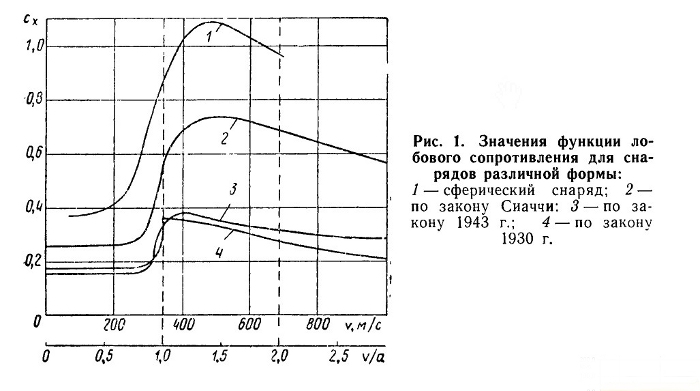

Значения функции лобового сопротивления для
снарядов различной формы

Рис. 1. Значения функции лобового сопротивления для снарядов различной формы:
1 — сферический снаряд; 2 — по закону Сиаччи: 3 — по закону 1943 г.; 4 — по закону 1930 г.
2,5 ч/а

В развитии ракетной техники ведущее место принадлежит русским и советским конструкторам и ученым. Первые удачные образцы боевых ракет были созданы в 1818 г. генералом русской артиллерии, участником Отечественной войны 1812 г. А. Д. Засядько. Им же были сконструированы станки для пуска ракет, некоторые из них позволяли вести залповый огонь шестью ракетами.
В середине XIX в. большой вклад в русскую ракетную технику внес генерал К. И. Константинов. Изготовленные под его руководством ракеты с успехом применялись во время Крымской войны 1853—1855 гг. В конструкции ракет было внесено большое количество оригинальных решений.
Теоретические основы движения ракет были заложены в трудах создателя механики тел переменной массы И. В. Мещерского и основоположника теории межпланетных полетов К. Э. Циолковского.
Началом плановых теоретических и экспериментальных исследований в СССР по ракетной технике можно считать работы Газодинамической лаборатории, организованной в 1921 г. в Москве. В 1931 —1933 гг. создаются группы по изучению реактивного движения (ГИРД), в которых работали энтузиасты ракетного дела Ф. А. Цандер, С. П. Королев, М. К- Тихомиров. А. А. Победоносцев и др. В начале 30-х годов были созданы первые боевые советские ракеты, с успехом применявшиеся (с некоторой доработкой) в годы Великой Отечественной войны. В настоящее время ракетная техника представляет собой могучую силу, способную решать задачи как тактического, так и стратегического характера.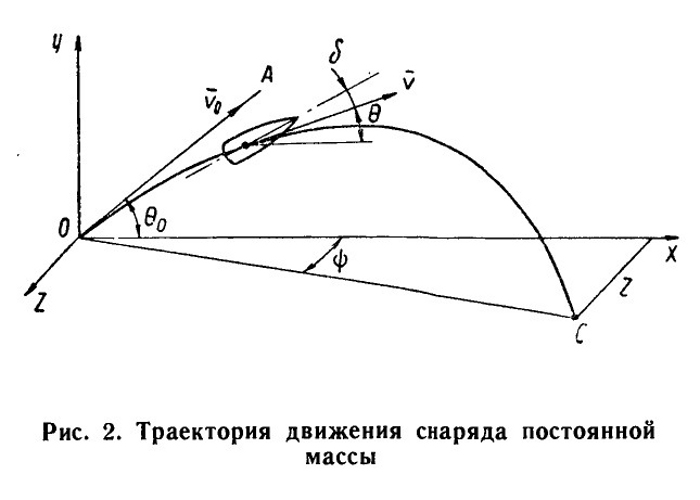

Рис. 2. Траектория движения снаряда постоянной массы

Внедрение ракетной техники послужило новым мощным толчком в развитии внешней баллистики. Целый комплекс задач, связанный с движением и управлением ракетами, с успехом решен советскими учеными.

3. основные понятия и определения

Центр масс снаряда описывает в пространстве траекторию (рис. 2). За начальную точку траектории во внешней баллистике принимают точку вылета, под которой понимают положение центра масс снаряда в момент, когда он теряет механическую связь х
со стволом. В точку вылета помещают начало неподвижной декартовой системы координат OXYZ. Горизонтальная плоскость OXZ, проведенная через точку вылета, называется горизонтом орудия, а вертикальная плоскость OYX, проходящая через вектор начальной скорости снаряда, — плоскостью стрельбы. Ось ОХ называется направлением стрельбы, линия OA, лежащая в плоскости OYX и проходящая через вектор начальной скорости, — линией бросания. Часть траектории от точки вылета О до вершины является восходящей ветвью, часть траектории, лежащая за вершиной, — нисходящей ветвью.
За точку падения С принимают точку пересечения траектории с горизонтом. Величина 2 отклонения снаряда от плоскости бросания называется деривацией.
В полете ось снаряда не совпадает с вектором скорости, а образует с ним угол нутации б. Плоскость, проходящую через ось снаряда и вектор скорости, называют плоскостью сопротивления. Двугранный угол, образованный плоскостями сопротивления и бросания, имеющий общей гранью вектор скорости, называют углом прецессии v (на рисунке не показан).